Physikalisch sucht man im Kontext der Frage “Wie viel wiegt die Luft?” die Masse der Erdatmosphäre. Eine ziemlich gute Abschätzung lässt sich schon mit wenigen Kenntnissen durchführen. Dabei ist es einerseits notwendig den mittleren Radius r der Erde zu kennen. Dieser beträgt r = 6.371 \, \mathrm{km} . Andererseits benötigt man den Zusammenhang zwischen dem Druck p , der Kraft F und der Fläche A , auf welche die Kraft einwirkt. Dabei gilt der Zusammenhang
p = \dfrac{F}{A} .
Der Druck ergibt sich also immer aus dem Verhältnis der einwirkenden Kraft F zur Fläche A . Dabei gilt:
- Je größer die Krafteinwirkung auf eine gegebene Fläche, desto größer auch der Druck.
- Umgekehrt gilt aber auch: Je kleiner die Fläche A ist, auf welche die Kraft F einwirkt, desto höher ist der Druck.
Als Beispiel hierfür dienen High-Heels. Diese haben meist einen sehr dünnen Absatz. Wird das ganze Körpergewicht darauf verlagert, so ergibt sich auf Grund der sehr kleinen Fläche ein derart hoher Druck auf den darunterliegenden Fußboden (vielleicht Parkettboden), sodass in diesen häufig Abdrücke bzw. Beschädigungen zurückbleiben.

Die Kraft bzw. Gewichtskraft F in Newton (\mathrm{N}) ergibt sich immer aus der Masse m und der Erdbeschleunigung g = 9,81 \frac{\mathrm{m}}{\mathrm{s^2}}:
F = m \cdot g .
Beispiel: Eine Person mit einer Masse von m = 70 \, \mathrm{kg} übt eine Kraft von F = 70 \, \mathrm{kg} \cdot 9,81 \frac{\mathrm{m}}{\mathrm{s^2}} = 686,7 \, \mathrm{N} auf den Erdboden aus.
Wie viel wiegt die Luft?
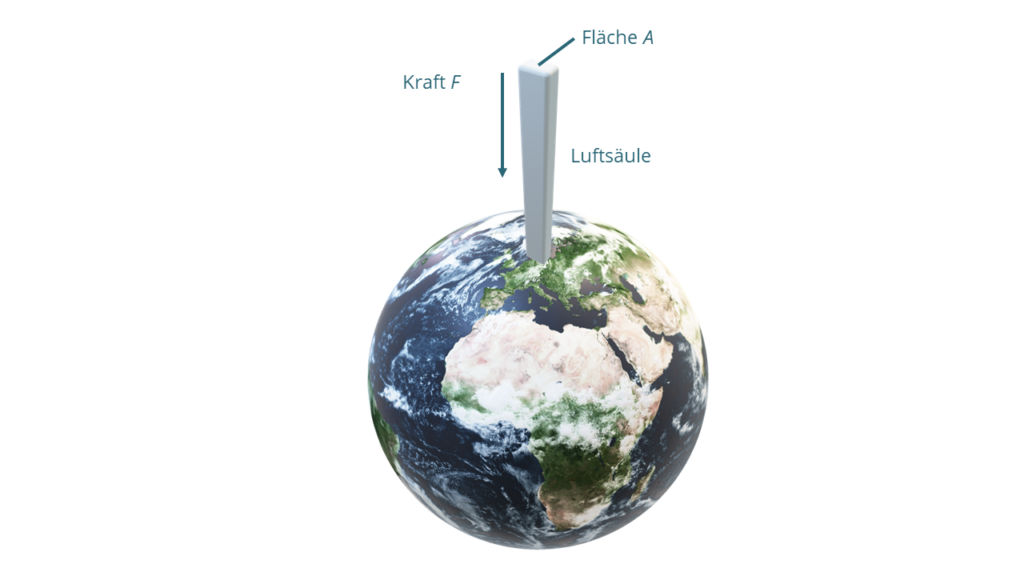
Wir spüren auf der Erdoberfläche den Luftdruck, ohne es häufig aktiv wahrzunehmen. Meist bemerkt man dieses erst, wenn er gerade nicht anwesend ist – beispielsweise in Flugzeugen oder auf Wanderungen in den Bergen. Grundsätzlich gilt, dass der Luftdruck mit der Höhe abnimmt. Dieser Luftdruck ergibt sich aus der über uns vorhandenden Luftsäule. Das kann man im Bild gut erkennen. Wenn man sich auf den Bergen oder im Flugzeug befindet, dann ist die Luftsäule natürlich nicht so hoch, als wenn wir uns auf Höhe des Meeresspiegels befinden würden. Aus diesem Grund ist der Luftdruck geringer, je weiter entfernt von der Erdoberfläche man sich befindet.
Diese Eigenschaft machen wir uns bei der Berechnung zu Nutze. Physikalisch wirkt auf Grund der Luftsäule eine Kraft F , welche auf der Erdoberfläche einen Luftdruck p erzeugt. Die Erdoberfläche stellt nun unsere Fläche A dar. Diese ist in guter Näherung eine Kugeloberfläche (A = 4 \cdot \pi \cdot r^2) . Mit dem mittleren Erdradius r = 6.371.000 \, \mathrm{m} ergibt sich eine Oberfläche von
\begin{array}{rl} A = 4 \cdot \pi \cdot r^2 &= 4 \cdot \pi \cdot 6.371.000^2 & \\ &=510 064 471 909 788 \, \mathrm{m^2} \\ &\approx 5,1 \cdot 10^{14} \, \mathrm{m^2} \end{array}
Damit können wir nun gemeinsam mit dem Normaldruck p = 101325 \, \frac{\mathrm{N}}{\mathrm{m^2}} die Kraft F berechnen, welche sich auf Grund der Luft ergibt:
F = p \cdot A = 101325 \, \frac{\mathrm{N}}{\mathrm{m^2}} \cdot 5,1 \cdot 10^{14} \, \mathrm{m^2}\approx 5,2 \cdot 10^{19} \, \mathrm{N}
Dies stellt die Krafteinwirkung in Newton (\mathrm{N}) dar. Möchten wir die Masse m berechnen, so müssen wir die Kraft F durch die Erdbeschleunigung g = 9,81 \frac{\mathrm{m}}{\mathrm{s^2}} dividieren. Wir erhalten
m = \dfrac{F}{g} = \dfrac{5,2 \cdot 10^{19} \, \mathrm{N}}{9,81 \frac{\mathrm{m}}{\mathrm{s^2}}} = 5,26 \cdot 10^{18} \, \mathrm{kg} .
Masse der Luft im Vergleich zur gesamten Masse der Erde
Die Masse der gesamten Luft m = 5,26 \cdot 10^{18} \, \mathrm{kg} ist nicht wirklich fassbar. Vergleichen wir ihn mit der Erdmasse von m_\text{Erde} = 5,98 \cdot 10^{24} \, \mathrm{kg} . Man erkennt, dass die Erdemasse über 1.000.000 = 10^6 Mal (1 Million Mal) soviel wie die Masse der gesamten Luft ist. Oder umgekehrt: Die gesamte Luft wiegt nur soviel wie 0,0001 \% der Erdmasse. Beide Massen verhalten sich in etwa wie die Masse einer Büroklammer (1 \, \mathrm{g}) zur Masse eines Kleinwagens (1.000 \, \mathrm{kg}) .


Eine kleine Anmerkung: Der berechnete Wert für die Masse der gesamten Luft m = 5,26 \cdot 10^{18} \, \mathrm{kg} ist etwas zu hoch. Dies liegt an der Tatsache, dass der Wasserdampf in der Berechnung nicht miteinbezogen wurde, denn feuchte Luft ist leichter also trockene Luft.



