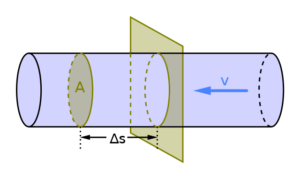
Die kinetische Energie eines Luftpakets
Ein Windrad wird, wie der Name schon verlautbart, durch den Wind angetrieben. Jedes Luftpaket hat dabei eine bestimmte Geschwindigkeit v und Masse \Delta m . Dadurch hat das Luftpaket eine kinetische Energie E_{\text{KIN}} = \dfrac{1}{2} \Delta m \cdot v^2. Setzt man für die Masse \Delta m die Dichte \rho und das Volumen \Delta V ein, so erhält man E_{\text{KIN}} = \dfrac{1}{2} \cdot \rho \cdot \Delta V \cdot v^2.
Die Leistung des Luftpakets
Jedes Windrad hat einen gewissen Durchmesser, sodass die Rotorblätter eine Fläche A überstreichen. In einer Zeit \Delta t geht durch diese Fläche ein Volumen
\Delta V = A \cdot \underbrace{v \cdot \Delta t}_{\text{Weg} \, \Delta s}
(Quelle: Lambda Geeks)
Wir möchten nun die Leistung des Luftpaketes berechnen. Die Leistung ist definiert als die Energie pro Zeiteinheit. Es ergibt sich für das Luftpaket eine Leistung
P_{\text{Luft}}= \dfrac{E_{\text{KIN}}}{\Delta t} = \dfrac{ \rho \cdot \Delta V \cdot v^2}{2 \cdot \Delta t} . Setzt man für \Delta V noch den zuvor erhaltenen Ausdruck ein, so erhält man für die Leistung des Luftpakets P_{\text{Luft}} = \dfrac{\rho \cdot A \cdot v^3}{2} . Die Energie eines jeden Luftpaketes, also des Windes, ist proportional zur dritten Potenz der Geschwindigkeit. Die bedeutet, dass eine Verdoppelung der Geschwindigkeit eine Verachtfachung der kinetischen Energie zur Folge hat.
Wie effizient ist ein Windrad?
Es ist nicht möglich, dass die gesamte Energie des Windes in Bewegungsenergie umgewandelt wird. Dies hat einen einfachen Grund:
Nehmen wir an die gesamte kinetische Energie würde durch das Windrad in elektrische Energie umgewandelt werden. Dann hätte ein Luftpaket nach dem Vorbeiströmen am Windrad keine kinetische Energie mehr und würde sich dementsprechend auch nicht bewegen. Das heißt: Die Luft nach dem Windrad würde still stehen. Dann können aber auch keine neuen Luftpakete mehr nachströmen und das Windrad käme zum Stillstand.
Das Luftpaket kann und soll nicht vollkommen abgebremst werden.
Vor dem Windrad
Vor dem Auftreffen auf die Anströmfläche des Windrades hat das Luftpaket eine Geschwindigkeit v_1 , sodass sich in einer Zeit \Delta t ein Volumen \Delta V = A_1 \cdot v_1 \cdot \Delta t durch die Fläche hindurchbewegt.
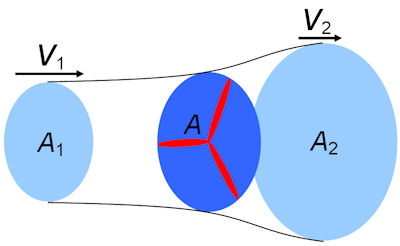
(Quelle: Universität Leipzig)
Nach dem Windrad
Eine ähnliche Gleichung können wir auch für den Bereich nach dem Windrad aufstellen. Da das Luftpaket Energie an das Windrad abgibt, ist die Geschwindigkeit v_2 < v_1 nach dem Windrad geringer als davor. Außerdem muss sich die durchströmte Fläche A_2 > A_1 vergrößern, damit nach dem Windrad dasselbe Volumen \Delta V = A_2 \cdot v_2 \cdot \Delta t ankommt. Die Leistung des Windrades ergibt sich aus der Differenz der Leistungen vor und nach dem Windrad, also:
P_\text{Nutz} = P_\text{vor} – P_\text{nach} = \dfrac{ \rho \cdot \Delta V \cdot (v_1^2-v_2^2)}{2 \cdot \Delta t} .
Diese Gleichung wollen wir noch ein wenig weiterentwickeln. In der Strömungsmechanik besagt das Theorem von Froude und Rankine, dass die Strömungsgeschwindigkeit in der Rotationsebene eines Rotors, Propellers oder einer Turbine sich als der Mittelwert der Strömungsgeschwindigkeiten hinreichend weit stromauf und stromabwärts ausdrücken lässt. Wir können in unserer Gleichung \Delta V = A_1 \cdot v_1 \cdot \Delta t = A_2 \cdot v_2 \cdot \Delta t durch \Delta V =A \cdot \dfrac{v_1 + v_2}{2} \cdot \Delta t ersetzen. Dies hat den Vorteil, dass dadurch die überstrichene Fläche der Rotorblätter A in der Gleichung auftaucht, und nicht die beiden unbekannten Flächen A_1 \, \text{und} \, A_2. Dadurch erhalten wir
P_\text{Nutz} = \dfrac{ \rho \cdot A \cdot (v_1 + v_2) \cdot (v_1^2-v_2^2)}{ 4} .
Nun können wir den Wirkungsgrad c_P berechnen:
\begin{array}{rl} c_P =& \dfrac{P_\text{Nutz}}{P_\text{Luft}} \\[2em] =& \dfrac{(v_1 + v_2) \cdot (v_1^2-v_2^2)}{ 2 \cdot v_1^3} \\[2em] =& \dfrac{(v_1 + v_2)}{v_1} \cdot \dfrac{(v_1^2-v_2^2)}{ 2 \cdot v_1^2} \\[2em] =& (1 + \dfrac{v_2}{v_1}) \cdot \dfrac{(1-\dfrac{v_2^2}{v_1^2})}{ 2} \\[2em] =& (1 + x) \cdot \dfrac{(1-x^2)}{ 2} \quad \text{mit} \; x = \dfrac{v_2}{v_1} \end{array}.
Dieser Ausdruck hat ein Maximum für x = \dfrac{1}{3}, sodass sich für den maximalen Wirkungsgrad c_P = \dfrac{16}{27} \approx 59 \% ergibt. Der Wirkungsgrad reicht fast an jenen eines Gas-und-Dampfkraftwerkes (GuD) heran, welches das effizienteste Kraftwerk bei Verwendung fossiler Brennstoffe darstellt. Zu diesen Gasturbinen wird es auch einen eigenen Beitrag geben, da sie den Ausstoß an \text{CO}_2 minimieren 450\, \text{g} \,\text{CO}_2-\text{eq}/\text{kWh}.
Woher habe ich meine Informationen?
Ich habe viele Informationen aus dem Buch Numbers don’t lie von Vaclav Smil. Dabei werden viele Themen der aktuellen Zeit wie Überalterung, Energiewende und Klimaschutz anhand von Zahlen und Fakten aufgearbeitet.